

力的合成和分解
一、标量和矢量
1.将数学量分辨为矢量和标量彰显了用分类方式研究化学问题的思想。
2.矢量和标量的根本区别在于它们遵照不同的运算法则:标量用代数法;矢量用平行四边形定则或三角形定则。
矢量的合成与分解都遵照平行四边形定则(可简化成三角形定则)。平行四边形定则实质上是一种等效替换的技巧。一个矢量(合矢量)的作用疗效和另外几个矢量(分矢量)共同作用的疗效相同,就可以用这一个矢量取代那几个矢量,也可以用那几个矢量取代这一个矢量,而不改变原先的作用疗效。
3.同仍然线上矢量的合成可转为代数法,即规定某一方向为正方向。与正方向相同的化学量用正号代入.相反的用减号代入,之后求代数和,最后结果的正、负彰显了方向,但有些数学量虽也有正负之分,运算法则也一样.但不能觉得是矢量力的正交分解,最后结果的正负也不表示方向如:功、重力势能、电势能、电势等。
二、力的合成与分解
力的合成与分解彰显了用等效的方式研究化学问题。
合成与分解是为了研究问题的便捷而引人的一种技巧.用合力来取代几个力时必须把合力与各分力脱钩,即考虑合力则不能考虑分力,同理在力的分解时只考虑分力而不能同时考虑合力。
1.力的合成
(1)力的合成的本质就在于保证作用疗效相同的前提下,用一个力的作用取代几个力的作用,这个力就是那几个力的“等效力”(合力)。力的平行四边形定则是运用“等效”观点,通过实验总结下来的共点力的合成法则,它给出了寻求这些“等效代换”所遵守的规律。
(2)平行四边形定则可简化成三角形定则。由三角形定则还可以得到一个有用的结论:假如n个力首尾相接组成一个封闭六边形,则这n个力的合力为零。
(3)共点的两个力合力的大小范围是
|F1-F2|≤F合≤F1+F2
(4)共点的三个力合力的最大值为三个力的大小之和,最小值可能为零。
【例1】物体遭到相互垂直的两个力F1、F2的作用,若两力大小分别为5
N、5N,求这两个力的合力.
解析:按照平行四边形定则做出平行四边形,如图所示,因为F1、F2互相垂直,所以做出的平行四边形为圆形,对角线分成的两个三角形为直角三角形,由勾股定律得:
N=10N
合力的方向与F1的倾角θ为:
θ=30°
点评:今后我们遇见的求合力的问题,多数都用估算法,即按照平行四边形定则做出平行四边形后,通过解其中的三角形求合力.在这些情况下作的是示意图,不须要很严格,但要规范,明晰什么该画虚线,什么该画实线,箭头应标在哪些位置等.
【例2】如图甲所示,物体遭到大小相等的两个拉力的作用,每位拉力均为200N,两力之间的倾角为60°,求这两个拉力的合力.
解析:按照平行四边形定则,做出示意图乙,它是一个矩形,我们可以借助其对角线垂直平分,通过解其中的直角三角形求合力.
N=346N
合力与F1、F2的倾角均为30°.
点评:
(1)求矢量时要注意除了要求出其大小,还要求出其方向,其方向一般用它与已知矢量的倾角表示.
(2)要学好化学,除把握化学概念和规律外,还要注意提升自己应用物理知识解决数学问题的能力.
2.力的分解
(1)力的分解遵守平行四边形法则,力的分解相当于已知对角线求邻边。
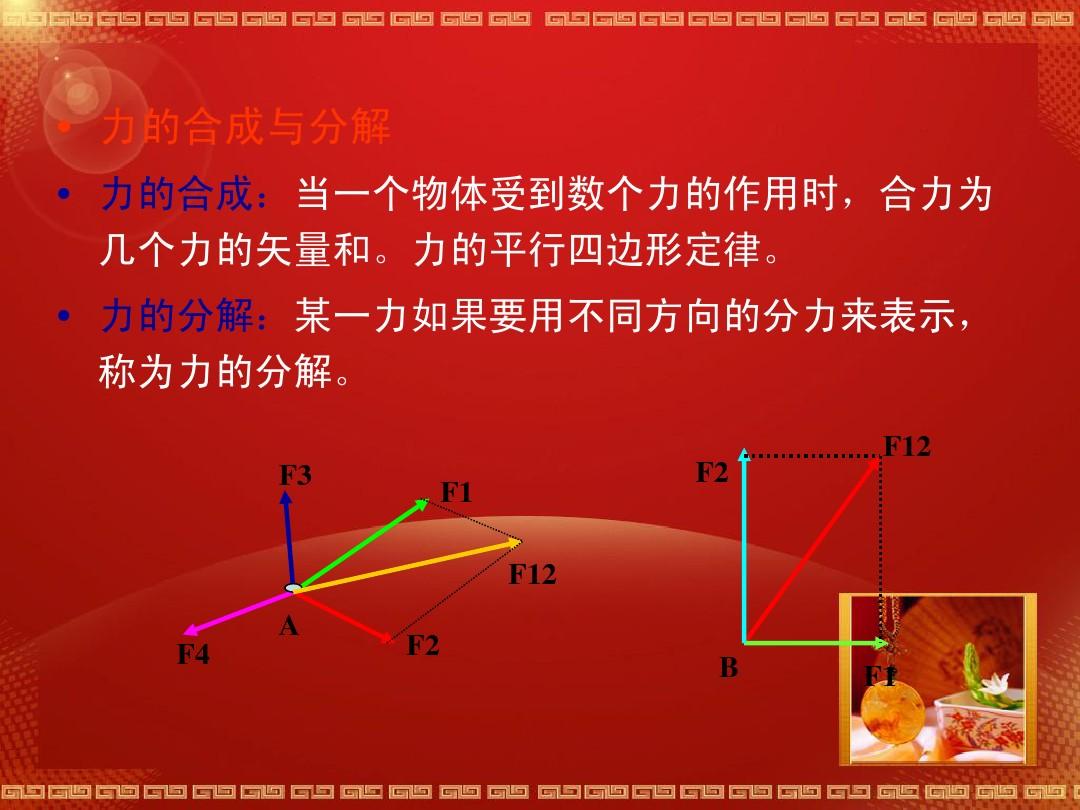
(2)两个力的合力唯一确定,一个力的两个分力在无附加条件时,从理论上讲可分解为无链表分力,但在具体问题中,应按照力实际形成的疗效来分解。
【例3】将置于斜面上质量为m的物体的重力mg分解为下降力F1和对斜面的压力F2,这些说法正确吗?
解析:将mg分解为下降力F1这些说法是正确的,而且mg的另一个分力F2不是物体对斜面的压力,而是使物体压紧斜面的力,从力的性质上看,F2是属于重力的分力,而物体对斜面的压力属于弹力,所以这些说法不正确。
【例4】将一个力分解为两个相互垂直的力,有几种分法?
解析:有无数种分法,只要在表示这个力的有向线段的一段任意画一条直线,在有向线段的另一端向这条直线做垂线,就是一种技巧。如图所示。
(3)几种有条件的力的分解
①已知两个分力的方向,求两个分力的大小时,有惟一解。
②已知一个分力的大小和方向,求另一个分力的大小和方向时,有惟一解。
③已知两个分力的大小,求两个分力的方向时,其分解不唯一。
④已知一个分力的大小和另一个分力的方向,求这个分力的方向和另一个分力的大小时,其分解方式可能唯一,也可能不唯一。
(4)使劲的矢量三角形定则剖析力最小值的规律:
①当已知合力F的大小、方向及一个分力F1的方向时,另一个分力F2取最小值的条件是两分力垂直。如图所示,F2的最小值为:F2min=Fsinα
②当已知合力F的方向及一个分力F1的大小、方向时,另一个分力F2取最小值的条件是:所求分力F2与合力F垂直,如图所示,F2的最小值为:F2min=F1sinα
③当已知合力F的大小及一个分力F1的大小时,另一个分力F2取最小值的条件是:已知大小的分力F1与合力F同方向,F2的最小值为|F-F1|
(5)正交分解法:
把一个力分解成两个相互垂直的分力,这些分解方式称为正交分解法。
用正交分解法求合力的步骤:
①首先构建平面直角座标系,并确定正方向
②把各个力向x轴、y轴上投影,但应注意的是:与确定的正方向相同的力为正,与确定的正方向相反的为负,这样,就用正、负号表示了被正交分解的力的分力的方向
③求在x轴上的各分力的代数和Fx合和在y轴上的各分力的代数和Fy合
④求合力的大小
合力的方向:tanα=
(α为合力F与x轴的倾角)
点评:力的正交分解法是把作用在物体上的所有力分解到两个相互垂直的座标轴上,分解最终常常是为了求合力(某一方向的合力或总的合力)。
【例5】质量为m的铁块在推力F作用下,在水平地面上做匀速运动.已知铁块与地面间的动磨擦质数为μ,这么铁块遭到的滑动磨擦力为下述各值的那个?
A.μmgB.μ(mg+Fsinθ)
C.μ(mg+Fsinθ)D.Fcosθ
解析:铁块匀速运动时遭到四个力的作用:重力mg、推力F、支持力FN、摩擦力Fμ.沿水平方向构建x轴,将F进行正交分解如图(这样构建座标系只需分解F),因为铁块做匀速直线运动,所以,在x轴上,向左的力等于往右的力(水平方向二力平衡);在y轴上向下的力等于向上的力(竖直方向二力平衡).即
Fcosθ=Fμ①
FN=mg+Fsinθ②
又因为Fμ=μFN③

∴Fμ=μ(mg+Fsinθ)故B、D答案是正确的.
小结:
(1)在剖析同一个问题时,合矢量和分矢量不能同时使用。也就是说,在剖析问题时,考虑了合矢量就不能再考虑分矢量;考虑了分矢量就不能再考虑合矢量。
(2)矢量的合成分解,一定要认真画图。在用平行四边形定则时,分矢量和合矢量要画成带箭头的虚线,平行四边形的另外两个边必须画成实线。
(3)各个矢量的大小和方向一定要画得合理。
(4)在应用正交分解时,两个分矢量和合矢量的倾角一定要分清那个是大锐角,那个是小锐角,不可随便画成45°。(当题目规定为45°时除外)
三、综合应用举例
【例6】水平横粱的一端A插在墙上内,另一端装有一小滑轮B,一轻绳的一端C固定于墙壁,另一端越过滑轮后悬挂一质量m=10kg的重物,∠CBA=30°,如图甲所示,则滑轮遭到绳子的斥力为(g=10m/s2)
A.50NB.50
NC.100ND.100
解析:取小滑轮作为研究对象,悬挂重物的绳中的弹力是T=mg=10×10N=100N,故小滑轮受绳的斥力沿BC、BD方向的大小都是100N,剖析受力如图(乙)所示.∠CBD=120°,∠CBF=∠DBF,∴∠CBF=60°,⊿CBF是等腰三角形.故F=100N。故选C。
【例7】已知质量为m、电荷为q的小球,在匀强电场中由静止释放后沿直线OP向斜下方运动(OP和竖直方向成θ角),这么所加匀强电场的场强E的最小值是多少?
解析:按照题意,释放后小球所受合力的方向必为OP方向。用三角形定则从下图中不难看出:重力矢量OG的大小方向确定后,合力F的方向确定(为OP方向),而电场力Eq的矢量起点必须在G点,终点必须在OP射线上。在图中画出一组可能的电场力,不难看出,只有当电场力方向与OP方向垂直时Eq才能最小,所以E也最小,有E=
点评:这是一道很典型的考察力的合成的题,不少朋友只死记住“垂直”,而不剖析哪两个矢量垂直,时常误觉得电场力和重力垂直,而得出错误答案。越是简单的题越要认真画图。
【例8】轻绳AB总长l,用轻滑轮悬挂重G的物体。绳能承受的最大拉力是2G,将A端固定,将B端平缓往右联通d而使绳不断,求d的最大可能值。
解:以与滑轮接触的那一小段绳子为研究对象,在任何一个平衡位置都在滑轮对它的压力(大小为G)和绳的拉力F1、F2共同作用下静止。而同一根绳子上的拉力大小F1、F2总是相等的,它们的合力N是压力G的平衡力,方向竖直向下。因而以F1、F2为分力做力的合成的平行四边形一定是矩形。借助矩形对角线相互垂直平分的性质,结合相像形知识可得
d∶l=
∶4,所以d最大为
【例9】A的质量是m,A、B仍然相对静止,共同沿水平面向右运动。当a1=0时和a2=0.75g时,B对A的斥力FB各多大?
解析:一定要审清题:B对A的斥力FB是B对A的支持力和磨擦力的合力。而A所受重力G=mg和FB的合力是F=ma。
当a1=0时,G与FB二力平衡,所以FB大小为mg,方向竖直向下。
当a2=0.75g时,用平行四边形定则画图:先画出重力(包括大小和方向),再画出A所受合力F的大小和方向,再依照平行四边形定则画出FB。由已知可得FB的大小FB=1.25mg,方向与竖直方向成37o角斜往右上方。
【例10】一根长2m,重为G的不均匀直棒AB,用两根细绳水平悬挂在天花板上,如图所示力的正交分解,求直棒重心C的位置。
解析:当一个物体受三个力作用而处于平衡状态,假如其中两个力的作用线相交于一点.则第三个力的作用线必通过前两个力作用线的相交点,把O1A和O2B延长相交于O点,则重心C一定在过O点的竖直线上,如图所示由几何知识可知:
BO=AB/2=1mBC=BO/2=0.5m
故重心应在距B端0.5m处。
【例11】如图(甲)所示.质量为m的球置于夹角为α的光滑斜面上,试剖析挡板AO与斜面间的夹角β为多大时,AO所受压力最小?
解析:尽管题目问的是挡板AO的受力情况,但若直接以挡板为研究对象,因挡板所受力均为未知力,将难以得出推论.以球为研究对象,球所受重力形成的疗效有两个:对斜面形成的压力N1、对挡板形成的压力N2,依据重力形成的疗效将重力分解,如图(乙)所示,
当挡板与斜面的倾角β由图示位置变化时,N1大小改变但方向不变,仍然与斜面垂直,N2的大小和方向均改变,如图(乙)中实线由图可看出挡板AO与斜面垂直时β=90°时,挡板AO所受压力最小,最小压力N2min=mgsinα。